- Szerző Matthew Elmers [email protected].
- Public 2024-01-11 07:41.
- Utoljára módosítva 2025-01-24 09:26.
Ebben a cikkben megpróbáljuk megérteni a Bayern, a Rivenge és a Pennsylvania csatahajók fegyvereinek páncélos behatolását, valamint a német, amerikai és brit páncél összehasonlító minőségét. Ezt rendkívül nehéz megtenni, mert az amerikai 356 mm-es, német 380 mm-es és brit 381 mm-es ágyúk adatai nagyon vázlatosak és hiányosak, és néha ellentmondanak egymásnak, de megpróbáljuk.
Mi a probléma pontosan? Lássuk, hogyan hasonlítja össze a haditengerészeti (és nem csak) történelem rajongóinak többsége bizonyos fegyverek páncélos behatolását. Például: egy, például angol dreadnoughteknak szentelt kiadványban olyan információk találhatók, amelyek szerint az első világháború brit 381 mm-es lövedéke körülbelül 70 kábel távolságban átszúrta a 381 mm-es páncéllemezt. Egy másik kiadásban, amely a már német "fővárosi" hajóknak szentelt - hogy egy hasonló német 380 mm -es lövedék 350 mm -es páncélt "sajátított el", mindössze 67, 5 kábellel. Ebből látszik következtetni, hogy az angol ágyú erősebb - pontosan ez a következtetés született.
A valóságban azonban az ilyen adatok ilyen módon történő összehasonlítása nagyon könnyen rendetlenségbe kerül.
A fenti adatokat tényleges lövés eredményeként szerezték -e be, vagy páncélos behatolási technikákkal számították ki? Ha ezek a tényleges lövöldözés eredményei, akkor mindkét fegyver esetében azonosak voltak a feltételek? Ha a páncél behatolását számítással nyertük, akkor ugyanazokat a módszereket alkalmazták? A kapott adatok az illetékes minisztériumok és osztályok szakemberei munkájának eredményei, vagy a számológépet előkészítő történészek számításainak eredményei? Világos, hogy a második esetben a pontosság sokkal alacsonyabb lesz … Nem kell messzire menni a példákért: vegyük S. Vinogradov híres monográfiáját, a "Superdreadnoughts of the Second Reich" Bayern "és a" Baden " ". A 2. számú mellékletben a tekintélyes történész V. L. A Kofman nagyszámú számítást végez, hogy összehasonlítsa a Rivenge és a Bayern csatahajók képességeit. De sajnos elég, ha megnézzük a 15 hüvelykes fegyverek paramétereinek táblázatát (124. o.), És látni fogjuk, hogy a tekintélyes szerzők számításai szerint egy angol 381 mm-es fegyver, amelynek magassági szöge 20, A 25 fok hatótávolsága mindössze 105 kábel, azaz körülbelül 19, 5 ezer m. Míg az azonos forrássebességű (732 m / s) és valamivel alacsonyabb emelkedési szög (20 fok) esetén a külföldi források lényegesen nagyobb távolságokat adnak - 21, 3-21, 7 ezer m. Természetesen azonban a valós értékektől való ilyen eltéréseknek van a legnegatívabb hatása a számítási eredményekre.
De még akkor is, ha a források bemutatják a szakemberek számításainak eredményeit, amelyek pontossága nem kétséges, felmerül egy másik tényező, amely bonyolítja az összehasonlítást: itt a páncél minősége a lényeg. Nyilvánvaló, hogy ugyanazok a britek, amikor egy adott dreadnought tervezésekor kiszámították a páncél penetrációját, a brit páncélzat megfelelő mutatóit használták, a németek - illetve a német stb. A különböző országok páncélja pedig tartósságukban különbözhet, de ez még mindig a fél baj: elvégre egyetlen országban ugyanazt a Krupp -páncélt folyamatosan fejlesztették. Így kiderül, hogy a tüzérségi rendszerek számításai, amelyeket például Angliában végeztek, és nyilvánvalóan ugyanazon Krupp -páncélzatra, de különböző időpontokban készültek, összehasonlíthatatlannak bizonyulhatnak. És ha ehhez hozzávesszük a páncéltok esetének fejlődésével kapcsolatos komoly munka szinte teljes hiányát a világ különböző országaiban …
Általánosságban elmondható, hogy a páncélok behatolásának többé -kevésbé megbízható összehasonlítása nem olyan egyszerű feladat, mint amilyennek első pillantásra tűnhet. És barátságos módon egy laikus (aki kétségkívül e cikk szerzője) jobb, ha nem foglalkozik ezzel az üggyel. De sajnos - mély sajnálatunkra, a profik valahogy nem sietnek ezekkel a kérdésekkel foglalkozni, így … ahogy mondani szokták, pecsétes papír hiányában egyszerű szöveget írunk.
Természetesen a fent említett tüzérségi rendszerek teljes körű tesztelését már nem lehet elvégezni, így sorsunk a számítások. És ha igen, akkor legalább néhány szót el kell mondani a páncélos penetrációs képletekről. Ha modern számítási módszereket tesznek közzé, akkor csak zárt kiadásokban és a népszerű irodalomban általában a Jacob de Marr formulát adják meg. Érdekes, hogy a Tengerészeti Akadémia professzora L. G. Goncsarov 1932 -es tüzérségi tankönyvében Jacob de Marr formulának nevezte. Ez a képlet sok mással együtt a múlt század elején elterjedt volt, és azt kell mondanom, elég pontos - talán még a legpontosabb is az évek hasonló képletei között.
Sajátossága abban rejlik, hogy nem fizikai, vagyis nem a fizikai folyamatok matematikai leírása. De Marr formulája empirikus, a vas- és acél-vaspáncél kísérleti ágyúzásának eredményeit tükrözi. Ennek a "tudománytalan természetnek" ellenére de Marr formulája jobban közelítette a lövés tényleges eredményeit és a Krupp páncélzatát, mint más általános képletek, ezért számításokra használjuk.
Az érdeklődők megtalálják ezt a képletet a cikk mellékletében, de nem kell mindenkit rákényszeríteni, hogy olvassa ezt az anyagot, hogy megértse - ez nem szükséges a cikk következtetéseinek megértéséhez. Csak azt jegyezzük meg, hogy a számítás nagyon egyszerű és ismerős fogalmakat használ minden katonai flotta története iránt érdeklődő számára. Ezek a lövedék tömege és kaliberje, a páncél vastagsága, a lövedék szöge a páncélhoz, valamint a lövedék sebessége, amikor a páncéllemezbe ütközik. De Marr azonban természetesen nem korlátozódhatott a fenti paraméterekre. Végül is a lövedék behatolása nemcsak a kaliberétől és tömegétől függ, hanem bizonyos mértékig az alakjától és az acél minőségétől is, amelyből készült. És a páncéllemez vastagsága, amelyet a lövedék képes leküzdeni, természetesen nemcsak a lövedék teljesítményétől, hanem a páncél minőségétől is függ. Ezért de Marr egy speciális együtthatót vezetett be a képletbe, amelyet valójában úgy terveztek, hogy figyelembe vegye a páncél és a lövedék jelzett tulajdonságait. Ez az együttható növekszik a páncél minőségének növekedésével, és csökken a lövedék alakjának és minőségének romlásával.
Valójában a különböző országok tüzérségi rendszereinek összehasonlításának fő nehézsége éppen ezen az együtthatón "nyugszik", amelyet a jövőben egyszerűen (K) fogunk nevezni. A fenti eszközök mindegyikéhez meg kell találnunk - ha természetesen némileg korrekt eredményt szeretnénk elérni.
Tehát először vegyünk egy meglehetősen széles körben elterjedt adatot a német Bayern 380 mm / 45-ös ágyú páncéljának behatolásáról, amely szerint a fegyver 12 500 m távolságban (ugyanazok a 67, 5 kábel) 350 mm páncél. Ballisztikus számológéppel találjuk meg a 750 kg-os lövedék paramétereit, kezdeti sebessége 800 m / s a páncélra ütközés pillanatában: kiderül, hogy egy ilyen lövedék egy szigorúan függőlegesen elhelyezett páncéllemezt üt 10, 39 fokos szögben, 505, 8 m / sec sebességgel. Egy kis felelősséget kizáró nyilatkozat - a továbbiakban, amikor a lövedék becsapódási szögéről beszélünk, az úgynevezett "normál szögből" értünk. "Normál" az, amikor a lövedék a felületére szigorúan merőleges, azaz 90 fokos szögben találja el a bonneplitet. Ennek megfelelően a lövedék 10 fokos szögben ütközött.a normálistól azt jelenti, hogy 80 fokos szögben ütközött a födémhez. felszínére, a "referencia" 90 foktól eltérve. 10 fokkal.
De térjünk vissza a német fegyver páncélos behatolásához. Az együttható (K) ebben az esetben megközelítőleg (a legközelebbi egész számra kerekítve) 2083 lesz - ezt az értéket teljesen normálisnak kell tekinteni az első világháború korszakának páncélzatánál. De itt egy probléma merül fel: a tény az, hogy a páncélok behatolására vonatkozó adatok forrása a "Második világháború német főhajói" című könyv, ahol a Bayern 380 mm / 45 lövegét hasonlították össze a csatahajó fő kaliberével. "Bismarck". És nem lehet, hogy a számítás figyelembe vette a két világháború közötti intervallumban létrehozott Krupp -páncél mutatóit, amely sokkal erősebb volt, mint a Bayenne -re, Rivenge -re és Pennsylvaniára telepített? Sőt, az elektronikus enciklopédia navweaps jelentése szerint bizonyíték van arra, hogy 20 000 m távolságban a német 380 mm-es kagylók képesek voltak áthatolni a 336 mm-es páncéllemezen, és az első világháború korszakának páncéljáról beszélünk.
Nos, hisszük: 20 km -nél a beesési szög 23,9 fok lesz, a lövedék sebessége a páncélon 410,9 m / s, és az együttható (K) - néhány szerencsétlen 1618, amely nem fér el a páncélban ellenállási értékek az első világháború minden korszakában. Hasonló eredmény általában közelebb hozza a német gyártmányú Krupp páncélt a homogén páncélellenálláshoz … Nyilvánvaló, hogy a navweaps adatok tartalmaznak valamilyen hibát.
Próbáljunk meg egy másik információforrást használni. Eddig a számított adatokat használtuk, és most megpróbáljuk összehasonlítani őket a német 380 mm / 45-ös ágyú tényleges vizsgálati eredményeivel: ezeket S. Vinogradov adta meg a fent említett német nyelvű monográfiában. csatahajók.
Leírja a páncéltörő lövedékekkel végzett 3 lövés következményeit, 200, 290 és 450 mm vastagságú páncéllemezek ellen, ez utóbbi a legérdekesebb számunkra: 734 kg súlyú lövedék 0 szögben találta el a páncéllemezt. (vagyis a felszínhez képest 90 fokos szögben) és 551 m / s sebességgel 450 mm -rel a födémen keresztül. Hasonló eredmény felel meg az együtthatónak (K) 1 913, de valójában valamivel alacsonyabb lesz, mert a németek akár 2 530 m -rel is megtalálták lövedéküket az általa átszúrt akadály mögött, és - általában. Sajnos, mivel nincs adatunk arról, hogy ebből a távolságból mennyit repült a lövedék a levegőben, mennyit "lovagolt" a földön, teljesen lehetetlen meghatározni az általa tárolt energiát a páncél behatolása után.
Vegyük most a brit 381 mm / 42 -es tüzérségi rendszert. Sajnos a páncélos penetrációjára vonatkozó adatok meglehetősen homályosak: például V. L. Kofman, megemlítik azt a tényt, hogy ezek a brit fegyverek páncélokat szúrtak ki, a saját kaliberük vastagságát körülbelül 70 kábel távolságban. De milyen lövedékkel és milyen kezdeti sebességgel? Figyelembe véve azt a tényt, hogy a hivatkozás szerepel a "Hood" harci cirkálónak szentelt monográfiában, és a hajó létrehozásának időszakára utal, feltételezhető, hogy 871 kg -os kagylóról beszélünk. Itt azonban felmerül egy másik kérdés: egy ilyen lövedék hivatalos kezdeti sebessége 752 m / s volt, de a britek néhány számítását alacsonyabb, 732 m / s sebességgel hajtották végre, tehát milyen értéket vegyünk? Bármelyik jelzett sebességet is választjuk, az együttható (K) 1 983 - 2 048 között ingadozik, és ez magasabb, mint amit a német fegyver (K) értékére számítottunk. Feltételezhető, hogy ez a brit páncél minőségének felsőbbrendűségéről beszél a némethez képest … vagy az, hogy a német lövedék geometriai alakja jobban megfelelt az áthatoló páncélnak? Vagy talán az egész lényege az, hogy V. L. A Kofman számított értékek, de a gyakorlatban a brit kagyló jobb eredményt érne el?
Nos, rendelkezésünkre állnak adatok a "Baden" csatahajó ágyúzásának eredményeiről

Tehát az egyik brit kagyló, 18 fokos szögben ütve. 472 m / sec sebességgel "felülkerekedett" a német főkaliberű torony 350 mm-es elülső páncélján. Ezek az adatok annál is értékesebbek, mert ebben az esetben nem brit, hanem német páncélzatot vetettek alá ágyúzásnak, vagyis a 381 mm / 42 és 380 mm / 45 lövegek tesztjei egyetlen koordináta-rendszerben vannak..
Sajnos nem segítenek nekünk túl sokat. Ha feltételezzük, hogy az angol héj a német tornyot átszúrta, ahogy mondani szokták, „az utolsó erővel”, és ha 351 mm -es páncélzat lenne, az kudarcot vallott volna, akkor az ő (K) értéke 2021 lenne. Érdekes egyébként, hogy S. Vinogradov kijelenti, hogy a brit lövedéket, amely áthatolt a német torony 350 mm -es frontpáncélján, később nem találták meg, de valójában a jelentés mást állít - felrobbant, és annak leírása, hogy a töredékek hova repültek a toronyban.
Természetesen nincs abszolút okunk feltételezni, hogy ez a behatolás volt a határ egy 381 mm-es lövedéknél, vagy akár annak közelében. Ennek ellenére bizonyos közvetett jelek alapján feltételezhető, hogy ez pontosan így volt. Egy másik találat erre „utal”: egy brit 871 kg -os lövedék 11 mm -es szögben 350 mm -es barbetet üt, bár 40 cm átmérőjű lyukat tudott készíteni a páncélzatba, de nem került a barbecet belsejébe magát, felrobbanva a páncél leküzdésének folyamatában. Ebben az esetben a találat szinte a barbet közepén történt, vagyis a páncéllemez görbülete, ha volt bármilyen hatása, akkor ez a minimum.
A fentiek összességéből megpróbálhatunk levonni néhány következtetést, de a bizonyítékbázis törékenysége miatt ezek természetesen nagyon sejtettek lesznek.
1. következtetés: Az első világháború alatti német páncélok tartósságukban nagyjából megegyeztek a britekkel. Ez a következtetés akkor érvényes, ha V. L. Kofman szerint a brit 381 mm / 42 -es ágyú képes volt 70 kbt kaliberű páncélt áthatolni, és ha nem tévedünk abban a feltevésben, hogy a német torony homloklemezének 350 mm -es behatolása 18 szögben fok és a sebesség 472 m / s … a brit 381 mm -es lövedék határa vagy nagyon közel van ahhoz.
Következtetés 2. Nyilvánvaló, hogy a német 380 mm-es lövedék alakja és minősége jobb páncéltörést biztosított, mint az angol. A fenti adatok alapján feltételezhetjük, hogy a brit 381 mm -es lövedék együtthatója (K) német páncélzatra lőve körülbelül 2000, míg a német 380 mm -es lövedék körülbelül 1900 volt. A brit és a német páncélzat páncélellenállása megközelítőleg egyenértékű, nyilvánvaló, hogy az alacsonyabb együttható (K) egyetlen oka csak maga a lövedék lehet.
Miért lehet jobb a német kagyló? A kaliber valamivel kisebb, egy milliméterrel, de természetesen ez aligha tud jelentős hatást kifejteni. A számítás azt mutatja, hogy azonos tömeggel (750 kg) a kaliber 1 milliméteres változása 1,03 milliméterrel növeli a páncél behatolását. A német lövedék is rövidebb - hossza 3,5 kaliber volt, míg a brit „Greenboy” hossza 4 kaliberű. Lehettek más különbségek is. Természetesen itt jelentős szerepet játszik az acél minősége, amelyből a lövedék készül.
Most számítsuk ki a német és a brit fegyverek páncélos behatolását 75 kábel távolságra - ez egy általánosan elfogadott távolság egy döntő ütközethez, ahol elegendő találatra lehet számítani a vonal ellenséges hajójának megsemmisítésére.
A megadott távolságban a brit 381 mm / 42 ágyú lövedéke 871 kg, 752 m / s kezdeti sebességgel lőtt, és a függőlegesen elhelyezett páncéllemezt 13,05 fokos szögben érte, sebessége pedig „a lemezen” 479,6 m / s volt … Ha (K) 2000, Jacob de Marr képlete szerint, a brit lövedék páncélos penetrációja 376, 2 mm volt.
Ami a német héjat illeti, minden egy kicsit bonyolultabb. Ha helyes az a következtetésünk, hogy a páncél penetrációját tekintve felülmúlta az angolt, akkor a német 380 mm / 45-ös ágyú képességei 75 kábelen nagyon közel álltak az angol tizenöt hüvelykes fegyverhez. Ezen a távolságon a német 750 kg -os lövedék 12,42 fokos szögben 482,2 m / s sebességgel találta el a célt, és (K) -nál 1900 -nál a páncél behatolása 368,9 mm volt. De ha ennek a cikknek a szerzője még mindig téved, és a német fegyver esetében érdemes ugyanazt az együtthatót használni, mint az angol fegyvernél, akkor a 380 mm-es lövedék képességei 342,9 mm-re csökkennek.
Ennek ellenére a szerző szerint a német lövedék páncéláthatolása a legközelebb van a 368, 9 mm -hez (elvégre a gyakorlati lövés 1913 -as együtthatót eredményezett, annak ellenére, hogy a lövedék akkor 2,5 km -t repült), de a páncél behatolása az angol lövedék kissé alacsonyabb lehet. Általánosságban elmondható, hogy 75 kábel távolságában a brit és a német tüzérségi rendszer meglehetősen összehasonlítható a páncél behatolása szempontjából.
De az amerikai 356 mm / 45 -ös fegyverrel minden sokkal érdekesebbnek bizonyult. Az orosz nyelvű szakirodalomban a korábban hivatkozott 680 kg súlyú kagylókra vonatkozó adatokat kanonikusnak kell tekinteni.
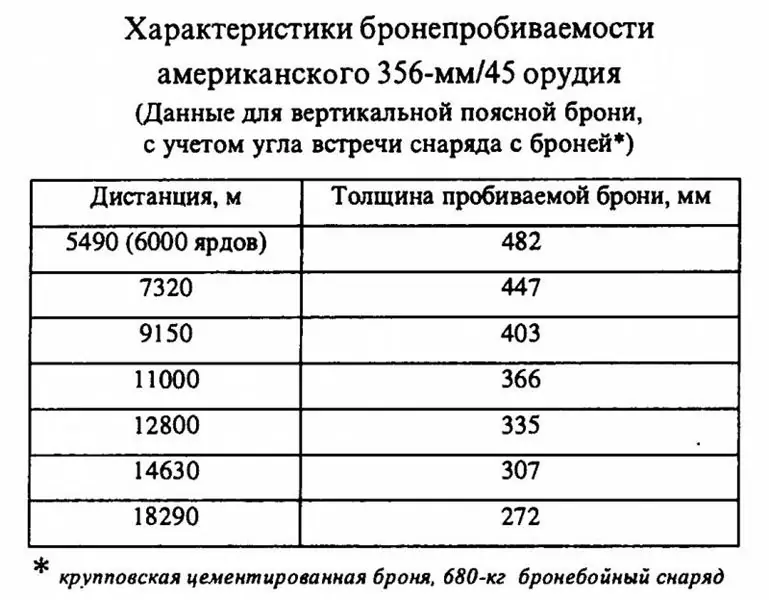
Ami azt illeti, az abban feltüntetett értékek teljesen nyilvánvaló következtetésekre vezetnek: ha még az Egyesült Államokban 1923 után megjelenő 680 kg-os kagylók is alacsonyabbak a páncélok áthatolásánál, mint a 380-381 mm-es európaiak. " kollégák ", akkor valójában mit beszélünk a korábbi 635 kg-os lövedékekről, amelyeket 356 mm-es amerikai dreadnough tüzérséggel szereltek fel! Könnyebbek, ami azt jelenti, hogy gyorsabban veszítenek sebességet repülés közben, miközben kezdeti sebességük nem haladta meg a nehezebb kagylókat, és alakját és minőségét tekintve az 1923 -as lőszer előnyösnek kell lennie. Világos, mint a nap, hogy az amerikai "Pennsylvania" a szolgálatba lépéskor rosszabb volt a páncélok behatolása tekintetében a brit és a német rettegésnél. Nos, nyilvánvaló, nem?
A szerző pontosan ezt a következtetést vonta le, figyelembe véve az amerikai tizennégy hüvelykes fegyverek képességeit az Egyesült Államok, Németország és Anglia "Standard" csatahajói cikkében. Amerikai "Pennsylvania" ". Aztán elővett egy számológépet …
A tény az, hogy a de Marra képlet szerinti számítás azt mutatta, hogy az amerikai 356 mm / 45-ös ágyúkon a táblázatban feltüntetett páncéltörés 2317-es együtthatóval (K) rendelkezett! Más szóval, a táblázatban látható amerikai 680 kg -os lövedékek mutatták az eredményeket, ha olyan páncélzatnak voltak kitéve, amelyet nem az első világháború korában, hanem sokkal későbbi és tartósabb mintákon hoztak létre.
Nehéz megmondani, hogy az első és a második világháború közötti időszakban mennyit nőtt a páncélvédelem ereje. Az orosz nyelvű forrásokban erre a kérdésre csak rövid és gyakran ellentmondó utalások találhatók, amelyek alapján feltételezhető, hogy Krupp páncéljának ereje mintegy 20-25%-kal nőtt. Így az első világ korszakának nagy kaliberű kagylói esetében az együttható (K) növekedése 1900-2000 -ről 2280-2500 -ra emelkedik, de itt emlékeznünk kell arra, hogy a páncélvédelem minőségének növekedésével természetesen a töltények minősége is megnőtt, és ezért a második világháború nehéz lőszerei (K) esetében kisebbek lehetnek. Ezért (K) a háború utáni kagylókra vonatkozó 2317 összegben, természetesen javítva, figyelembe véve a korábban szerzett tapasztalatokat, meglehetősen organikusnak tűnik, de a második világháború korszakának páncélzata szempontjából nem az első.
De ha az együtthatót (K) az amerikai 680 kg-os kagylókra 2000-re állítjuk, vagyis a páncélvédelem minőségét az első világháború korába visszük, 75 kábel távolságra páncélt kapunk áthatolás 393,5 mm szinten, vagyis magasabb, mint a brit és német tizenöt hüvelykes fegyvereknél!

A 635 kg -os lövedékre való átalakítás nagyon jelentéktelen korrekciót eredményez - a ballisztikus számológép azt mutatta, hogy 75 kábel távolságban, beesési szöge 10, 82 fok. és a sebesség "a páncélon" 533, 2 m (K) -on 2000 -vel egyenlő, az amerikai lövedék áthatol az első világháború korszakának páncélján, 380 mm vastag, vagyis lényegesen több, mint a saját kaliber!
Másrészt teljesen lehetséges, hogy egy ilyen számítás még mindig nem teljesen helyes. A tény az, hogy egyes jelentések szerint ugyanazon páncélzat együtthatója (K) csökken a lövedék kaliberének növekedésével. Így például számításainkban a számítással nyert és a forrásokban közzétett német 380 mm / 45 tüzérségi rendszer maximális értéke (K) 2083. Ugyanakkor a német 305 mm-es számítások / 50 lőfegyver, amelyeket a Heligolanddal kezdődő Kaiserlichmarine hajókra szereltek fel, a páncélok behatolására vonatkozó források adatai (K) 2145 szinten vannak. Ennek megfelelően lehetséges, hogy a 356 mm / 45 löveg (K) = 2000 Az amerikai fegyverek páncéljának áthatolása még mindig túl kicsi.
Ezen túlmenően sajnos a szerzőnek nincsenek "nyomai" ahhoz, hogy összehasonlítsák az amerikai Krupp páncélzat páncélállóságát európai társaival. Nincs más hátra, mint a német és angol páncélvédelemmel egyenértékűnek tekinteni, bár ez persze nem biztos, hogy így van.
Foglaljuk össze ezeket a meglehetősen kaotikus adatokat. Figyelembe véve a számítások során használt "módszerek" hibáit, nagy valószínűséggel feltételezhető, hogy A Rivenge, a Bayern és a Pennsylvania csatahajók fő kaliberű ágyúinak függőleges páncélvédelmének páncélos behatolása 75 kábel távolságban megközelítőleg azonos volt, és megközelítőleg 365-380 mm.
Egy csomó feltevés ellenére a rendelkezésünkre álló adatok továbbra is lehetővé teszik számunkra, hogy következtetéseket vonjunk le a függőleges páncélvédelemmel kapcsolatban. De a vízszintes korlátok áttörésével, amelyek páncélozott fedélzetek, minden sokkal bonyolultabb. A helyzet az, hogy Jacob de Marr sajnos egyáltalán nem foglalkozott azzal, hogy megalkosson egy képletet a vízszintes védelem erősségének meghatározására. A modern páncéltípusokhoz igazított alapformulája csak 75 mm feletti vastagságú cementált páncél kiszámítására alkalmas. Ezt a képletet a cikk 1. számú függeléke tartalmazza, és a cikk összes korábbi számítása ezzel készült.
De az akkori hajók fedélzetét nem cementált (heterogén), hanem homogén páncélzat védte, amelyből hiányzott a felületi edzett réteg. Az ilyen páncéloknál (de - függőlegesen felszerelve!) Egy másik képletet használnak, amelyet 75 mm -nél kisebb vastagságú nem cementált páncéllemezek értékelésére szántak, ezt a 2. függelék tartalmazza.
Szeretném megjegyezni, hogy mindkét képlet több mint komoly forrásból származik: „A haditengerészeti taktika menete. Tüzérség és páncél 1932, szerző - az RKKA Tengerészeti Akadémia professzora L. G. Goncsarov, a háború előtti Szovjetunió egyik vezető szakértője a haditengerészeti tüzérség területén.
És sajnos egyikük sem alkalmas a vízszintes védelem tartósságának felmérésére. Ha a cementált páncél képletét használjuk, akkor 75 kábel távolságban szűkös páncél-áthatolást kapunk: 46,6 mm 381 mm / 42 brit, 39,5 mm 380 mm / 45 német és 33,8 mm 356 mm / 45 amerikai esetén fegyverek. Ha a második formulát alkalmazzuk a nem cementált páncélra, akkor azt kapjuk, hogy amikor 75 kábel távolságra jellemző szögben ütik, mindhárom tüzérségi rendszer könnyen áthatol a 74 mm -es páncéllemezen, és ezután hatalmas kinetikus energia -ellátást tart fenn - például az angol 381 mm-es lövedék, amely 75 kábel távolságban ilyen vastagságú páncélzatba hatol be, 264,5 m / s, míg sebessége 482,2 m / s lesz. Ha figyelmen kívül hagyjuk a páncéllemez vastagságának korlátozását, kiderül, hogy a brit 381 mm-es lövedék a fenti képlet szerint képes áthatolni a fedélzeti páncélzaton, amelynek vastagsága meghaladja a 180 mm-t! Ami persze teljesen lehetetlen.
Ha megpróbálunk hivatkozni a Bayern-osztályú csatahajó vizsgálati eredményeire, látni fogjuk, hogy a páncéltörő 871 kg-os brit kagyló kétszer találta el a tornyok vízszintes páncélzatát, amelynek vastagsága 11 fokos szögben 100 mm volt, ami 67,5 kábel távolságnak felel meg 752 m / s kezdősebességű lövedék és 65 kábel esetén - 732 m / s kezdősebességű lövedék esetén. Mindkét alkalommal nem szúrták ki a páncélt. De egy esetben a lövedék, ricocheting, hornyot készített a páncélba 70 cm mélységgel, vagyis a lemez nagyon erősen hajlott. És a másodikban, bár a héj ismét rikocézett, a páncélzat nemcsak 10 cm -es homorú volt, hanem szakadt is.

A kár hasonló jellege azt sugallja, hogy bár a német 100 mm -es páncélzat a megadott távolságokon védelmet nyújtott, ha nem is a lehetséges határon, akkor nagyon közel volt ahhoz. De a cementált páncél képlet szerinti számítás csak 46,6 mm -es páncél penetrációt eredményez nagyobb távolságban, ahol a beesési szög nagyobb lesz, és ennek megfelelően könnyebb lenne a lövedék behatolni a fedélzeti páncélba. Vagyis a képlet szerint kiderül, hogy a 100 mm -es fedélzetnek viccesen és nagy biztonsági tartalékkal kellett volna tükröznie az angol kagylókat - a gyakorlat azonban ezt nem erősíti meg. Ugyanakkor a nem cementált páncél képletét használó számítások szerint kiderül, hogy a badeni fő kaliberű tetőket könnyen át kellett volna lyukasztani, és - nagy mennyiségű kagylóenergiával -, ami ismét nem egyáltalán megerősítette a gyakorlat.
Azt kell mondanom, hogy a számítások ilyen pontatlanságai teljesen logikusak. Amint azt korábban említettük, de Marr képletei nem a fizikai folyamatok matematikai leírása, hanem csak a páncél tesztelésekor kapott minták rögzítése. De a függőleges, nem vízszintes páncélvédelmet tesztelték, és egyáltalán nem meglepő, hogy a minták ebben az esetben egyszerűen leállnak: vízszintesen elhelyezett páncélok esetében, amelyekbe a héjak nagyon kis szögben ütköznek a felületükkel szemben, ezek a minták, természetesen teljesen mások.
Ennek a cikknek a szerzője olyan véleményekkel találkozott "az interneten", hogy de Marr képletei hatékonyan működnek a normától való eltérés szögeinél, amelyek nem haladják meg a 60 fokot, azaz 30 fokot a födém felületétől és így tovább. Feltételezhető, hogy ez az értékelés nagyon közel áll az igazsághoz.
Így sajnálattal kell megállapítanunk, hogy a szerző rendelkezésére álló matematikai berendezés nem teszi lehetővé a Rivenge, Bayern és Pennsylvania csatahajók vízszintes védelmi ellenállásának megbízható számításait. A fentiekre tekintettel nehéz lesz felhasználni a vízszintes páncélok páncélos áthatolására vonatkozó, különböző forrásokból származó adatokat - általában ezek mindegyike ugyanazokon a számításokon alapul de Marr képletei szerint, és helytelenek.






