- Szerző Matthew Elmers [email protected].
- Public 2023-12-16 22:14.
- Utoljára módosítva 2025-01-24 09:26.

Ebben a cikkben megpróbáljuk meghatározni az első világháborúból származó orosz páncélok tartósságát. Ez a kérdés rendkívül nehéz, mert rendkívül rosszul foglalkozik az irodalommal. És a lényeg ez.
Köztudott, hogy a 19. század végén a hadihajók építésében vezető tengeri hatalmak a Krupp -módszerrel készített páncélzatra álltak át. De ez egyáltalán nem jelenti azt, hogy azóta ezen országok hajóinak páncélzata egyenértékűvé vált.
A helyzet az, hogy Krupp páncéljának "klasszikus receptje" (más néven "minőségi 420", 1894 -ben megalkotva) nem maradt változatlan, hanem javult. Legalábbis olyan országok szerint, mint Anglia és Németország. De mennyire tökéletesítette magát, és milyen eredményeket értek el a különböző hatalmak páncélmesterei - ezt sajnos nem tudom biztosan.
Tűzpróba
Az orosz páncél lövedékállósága elfogadható pontossággal határozható meg, köszönhetően a régi "Chesma" csatahajó kísérleti ágyúzásának, amelyet "kizárt hajónak" minősítettek. A hajón egy kísérleti rekeszt hoztak létre, amely lemásolta a Szevasztopol-osztályú dreadnough-ok különböző részeinek védelmét, és a kísérlet tisztasága érdekében sok olyan eszközzel is fel volt szerelve, amelyekkel rendelkezniük kellett volna. Így például a kazamatákba gőzcsöveket (amelyek ott haladtak csatahajókon), lőfegyvereket, tűzvédelmi eszközöket és elektromos vezetékeket stb.

Ezután a kísérleti rekeszt különböző 6 és 12 hüvelyk közötti kaliberű lőszerekkel hántolták, beleértve természetesen a legújabb 305 mm-es páncéltörő és robbanásveszélyes lövedékeket is. Ennek ellenére a vizsgálati jelentések nagyon teljesek, ahogy az ilyen esetekben kell. Nemcsak az ütés következményeinek leírását tartalmazzák, hanem a lövedék sebességét is a páncél ütés pillanatában, valamint a lövedék és a páncél találkozási szögét.
Mindez lehetővé teszi számunkra, hogy kiszámítsuk az orosz páncélok ellenállását a legújabb hazai 470, 9 kg -os kagylók vonatkozásában, ugyanazon Jacob de Marr képlet szerint, amelyet korábban többször idéztem. De idézem még egyszer, hogy a kedves olvasónak ne kelljen a korábbi cikkeket végiglapoznia. A lövedék minőségének és a páncél tartósságának arányát ebben a képletben a "K" együttható írja le. Sőt, minél magasabb ez az együttható, annál erősebb a páncél.

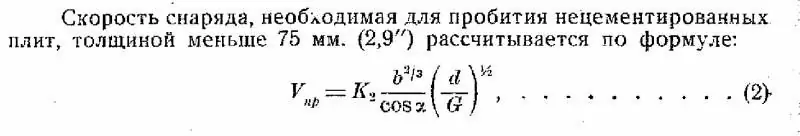
Az orosz páncélzat értékelésének bizonyos nehézségét az okozza, hogy elsősorban a kagylókat tesztelték, és nem a legújabb dreadnoughtek védelmének végső páncélállósága. Úgy tűnik - mi a különbség? De valójában nagyon jelentős. Amikor a lövedékeket tesztelik, az érdekük, hogy megbízhatóan megsemmisítsék a páncélt a fő harctávolságon. Amikor a páncélt kipróbálják, érdeklődés mutatkozik a végső feltételek mellett, amelyekben továbbra is megvédheti a hajót.
Mindazonáltal a "4. számú hajón kizárt hajó" találatainak statisztikái továbbra is lehetővé teszik bizonyos következtetések levonását.
250 mm -es páncélzatról való tüzelésről
Sajnos a 125 mm -es vagy annál kisebb páncélütések számunkra nem érdekesek - minden esetben kiderült, hogy vagy a lövedék energiája elegendő volt ahhoz, hogy áthatoljon rajta, vagy az ütési szög olyan kicsi volt, hogy geller. Más szóval, a páncél tartósságának meghatározásához a 125 mm -es és az alatti páncélütések statisztikái haszontalanok.
Más kérdés a vastag 225 és 250 mm -es páncélzatok ütése, amelyeket közelebbről megvizsgálunk.
Kezdjük 250 mm -es páncélzattal, amely a "4. számú hajó" kifutótornyának falait védte. Összesen 13 lövést adtak le erre a kormányállásra, de némelyiket a tetőre, másokat erősen robbanásveszélyes lövedékek. A páncéltörő lövedékeket csak 5-ször lőtték 250 mm-es páncélokra.
A legerősebb lövés a 6. szám volt (a tesztjelentések szerint számozva). Egy 305 mm-es páncéltörő lövedék 557 m / s sebességgel 80 ° -os szögben (10 ° -kal a normálistól) érte a páncéllemezt. Egy lövedék hasonló sebessége 470, 9 kg lenne, mindössze 45 kábel távolságában. Igaz, a normálistól való eltérés szöge kisebb lenne - 6, 18 °.
A páncél természetesen átfúrta a páncélt. Tartásához több mint 2700 "K" páncélra lenne szükség. És ez túlzott érték, még a második világháború sokkal fejlettebb páncélzatának mércéje szerint is. Az általam végzett számítások azt mutatják, hogy távolról az orosz 305 mm / 52 pisztoly mod. 1907 behatolhat a 433 mm -es Krupp páncéllemezébe, "minőségi 420".
A fennmaradó 4 lövés egyenlő feltételek mellett történt. A lövedék sebessége a páncélon 457 m / s volt, az akadályokkal való találkozás szögei körülbelül 80 ° (eltérés a normál 10 ° -tól). Számításaim szerint az orosz kagylók ilyen sebességgel rendelkeznének 75 kábel távolságban, de az akadályokkal való találkozás szöge rosszabb lenne - 76, 1 ° (eltérés a normálistól - 13, 89 °). Ilyen körülmények között a fenti számítások szerint 285,7 mm Krupp páncél hatolt be (K = 2000). De a valóságban minden nem olyan egyértelműnek bizonyult.
A 11. lövés során minden simán ment. A páncéltörő felülkerekedett a 250 mm-es páncéllemezen, nekicsapódott a kormányállás szemközti falának, és már ekkor felrobbant, így az ütközés helyén kátyú keletkezett 100 mm mélységben. A 10. lövésnél a páncél is eltört. De nem teljesen világos, hogy pontosan mikor történt a héj kitörése - ezt a jelentés nem jelzi. De nyilvánvalóan ez történt a konttorony belsejében, mert a robbanás ereje leszakította a tető páncéllemezeit, és a szomszédos 250 mm-es lemezt egyszerűen kiszakították a tartóelemekből és bevetették.

Így ezzel a lövéssel a lövedék nettó behatolását és áthaladását a páncélvédelem egészéhez kell számítani.
De a 9. lövésnél egy kis incidens történt - a héj közvetlenül a 70 mm -es padlóval szemben találta el a páncélt. Ennek eredményeként a 250 mm-es páncéllemezt átszúrták, és körülbelül 450x600 mm méretű sarka letört, és a 70 mm-es padlóban 200 mm hosszú kátyút találtak. Ezért vitatható, hogy ebben az esetben is a lövedék nem csak a páncélt szúrta át, hanem tisztességes energiával tette, ami elég volt ahhoz, hogy egy vízszintesen elhelyezkedő 70 mm-es páncél acéllemezt károsítson.
Ennek megfelelően az öt találatból négyben az orosz páncéltörő lövedékek a várt eredményt mutatták, amit de Marr számításai is megerősítenek. De a # 7 lövés során furcsa dolog történt - a lövedék pontosan ugyanúgy találta el a páncéllemezt, ugyanabban a 80 ° -os szögben és azonos sebességgel, 457 m / s sebességgel, de nem szúrta át a páncélt, felrobbant annak átjárása. Ennek eredményeként kiderült egy 225-250 mm mélységű kátyú: csak "16 kg-ig terjedő héjtöredékek".
Látjuk, hogy a 305 mm-es páncéltörő kagylók 4 ütéséből, amelyeknek 285 mm vastag páncélzaton kellett volna áthatolniuk, csak 3 volt „tiszta” behatolás. Egy esetben a héj felrobbant, miközben áthaladt a páncélon, bár nem volt.
Mi az oka ennek a fiaskónak? Talán maga a kagyló? Tegyük fel, hogy a hibás biztosíték idő előtt működött. De lehetséges egy másik értelmezés is: a tény az, hogy a páncél egy lövedék által való behatolása valószínűségi jellegű. Vagyis nincs olyan, hogy például ha a Jacob de Marr -formula szerint a lövedékkel áthatolt páncél maximális vastagsága bizonyos körülmények között 285 mm, akkor a 286 mm -es páncélt nem fogják áthatolni. a lövedék mindenképpen. Lehet, hogy áttör. És fordítva - törje meg azonos körülmények között kisebb vastagságú páncélok ellen.
Más szóval, maga a Jacob de Marr formula (vagy bármely más analógja) egyáltalán nem rendelkezik farmakológiai pontossággal. A valóságban egész tartományok léteznek, amelyekben egy páncéllemezt bizonyos szögben és sebességgel ütő lövedék bizonyos valószínűséggel behatolhat a páncélba, de ez nem számítható ki általánosan elfogadott páncéláthatolási képletekkel. És könnyen lehet, hogy a 7. számú lövés esetében a fent említett valószínűség működött.
Így véleményem szerint a # 7. Lövés eredményei véletlenszerűek, és nem kell őket figyelembe venni. És a 250 mm vastagságú orosz dreadnoughtok páncélja nem tudta elviselni azt, hogy 450 m / s sebességgel 470, 9 kg lövedék és körülbelül 80 ° -os akadály ütközési szöge találta el. De Marr szerint kiderül, hogy az orosz páncél "K" együtthatójának ebben az esetben 2228 alatt kell lennie. De mennyit?
Véleményem szerint a válasz a 11. számú lövés következményeinek elemzésével kapható. A kör 250 mm-es lemezt szúrt, a szemközti falnak ütközött, és ott 100 mm-es kátyút készített. Ezért feltételezhetjük, hogy a fenti paraméterekkel rendelkező orosz 470,9 kg -os lövedék maximális páncél -áthatolása 250 mm volt Krupp cementált páncélzatánál. És további 100 mm -es, egyenetlen, homogén páncél.
Miért homogén? A tény az, hogy mint tudják, a cementált páncél két rétegből áll. A felső nagyon erős, de ugyanakkor törékeny, majd lágyabb, de viszkózusabb páncél kezdődik. A lövedék, amely a 250 mm-es páncéllemezt találta el, a kormányház belsejéből a „puha és viszkózus” réteget találta el, amely tulajdonságaiban inkább hasonlít a homogén, mint a cementált páncélhoz.
Ezenkívül figyelembe kell vennie, hogy a páncél egészén áthaladó és mögötte felrobbanó lövedék "K" együtthatóját számolom. A 11. számú lövés esetében azonban nem ez történt - a kagyló, amely áttörte Krupp 250 mm -es cementpáncélját, és a második lemez hátulját találta el, nem szúrta át a páncélt, hanem felrobbant, és csak A robbanás energiáját figyelembe véve 100 mm-es kátyút sikerült kialakítani. Így a "250 mm -es cementált + 100 mm -es homogén páncél" számítását tekinthetjük olyan feltételezéseknek, amelyek nyilvánvalóan kedvezőtlenek a páncél számára. Ennek megfelelően a kapott eredmény tekinthető a minimumnak, amely alatt az orosz gyártmányú Krupp páncél ellenállása nem lesz.
És akkor a számítás nagyon egyszerű. A lövedék sebessége, mint fentebb már sokszor elhangzott, 457 m / s, a normálistól való eltérés szöge, amikor a 250 mm -es páncéllemezt érinti, 10 °. Amikor áthalad ezen a páncélon, a lövedék "megfordul", és már 90 ° -os szögben, azaz 0 ° -os eltéréssel találja el a második lemezt. Ez a 9. ábrából következik: „„ A haditengerészeti taktika menete. Tüzérség és páncél "L. G. Goncsarov, a 132. oldalon. Ahol a lövedékek ütés közbeni erősségei mellett a páncélon való áthaladás grafikonja is látható, a páncélon való találkozás szögétől függően.
Az orosz homogén és cementált páncélzat páncélállóságának aránya számomra ismeretlen. De G. Evers szerint a német cementált páncél "K" együtthatója 23% -kal magasabb, mint a homogén. És valószínűleg az orosz páncélok esetében ez az arány is igaz. Ezenkívül figyelembe kell venni, hogy amikor áthalad egy 250 mm-es páncéllemezen, a lövedék elveszíti páncéltörő sapkáját. Ez éppen ellenkezőleg, a "K" homogén páncélzat 15%-os növekedéséhez vezet.
A lövedék sebességének kiszámításakor, hogy áthatoljon egy 100 mm-es homogén lemezen, ugyanazt a képletet alkalmazták, mint egy 250 mm-es cementált lemeznél, csak a "K" együtthatót változtatták meg. Tudom, hogy L. G. Goncsarov azt javasolta, hogy a homogén páncélzathoz más formulát használjon, amelyet saját tankönyve adott. De szerinte 75 mm -nél vékonyabb páncéllemezekhez tervezték. Végül is van 100 mm. Ezenkívül G. Evers szerint Jacob de Marr fenti képletének alkalmazása homogén páncélokra is alkalmazható.
A cementált orosz páncélzat "K" számítási eredményei szerint a 2005 -nek van értéke. Most nézzük meg, hogy voltak -e olyan esetek a forgatás során, amelyek cáfolják ezt az eredményt.
225 mm -es páncélzatról való tüzelésről
A 225 mm-es páncélzatra mindössze 2 páncéltörő lövedéket lőttek ki. Ezenkívül a lövedék sebessége a páncéllal való érintkezés pillanatában akár 557 m / s volt - ilyen sebességgel kellett volna a lövedéknek 45 kábel távolságban lennie. Igaz, a páncéllal való találkozás szöge nagyon hátrányos volt - 65 ° vagy 25 ° eltérés a normálistól. De még ebben az esetben is, annak érdekében, hogy ellenálljon a 470, 9 kg lövedék ütésének, a páncéllemeznek "K" együtthatóval kell rendelkeznie 2690 felett. Ami természetesen teljesen lehetetlen. Más szóval, amikor ilyen paraméterekkel tüzelnek, még a második világháborús korszak páncélzatát is át kellett szúrni a lövedék hatalmas energiaellátásával.
A 25. lövéssel pedig pontosan ez történt. A héj könnyen átszúrta a 225 mm-es páncéllemezt (nem is tört át, hanem egyszerűen kitört belőle egy 350x500 mm-es darabot), majd ütközött egy kúphoz, amely 25 mm-es páncélból állt egy 12 mm-es fémen szubsztrátumot, és 1x1, 3 lyukat csinált benne m. A lövedék kitörésének pontos helyét nem állapították meg. De feltételezték, hogy bement a gépházba, és már ott felrobbant. Más szóval, az eredmény pontosan az volt, amit egy ilyen ütéssel el lehetett várni.
De a második körrel (27. sz. Lövés) minden érthetetlennek bizonyult. A lövedék eltért a célponttól. És ahogy a jelentés mondja: "üsd a páncél felső szélét". A lövés eredményét könnyebb idézni a dokumentumból:
„A lövedék mintegy 75 mm mély és körülbelül 200 mm széles kátyút csinált a páncélban, és az ing kiálló szélét négyzettel letépve itt lassítás nélkül felrobbant, és fekete füstöt bocsátott ki. A 2. számú kazemata nem sérült meg."
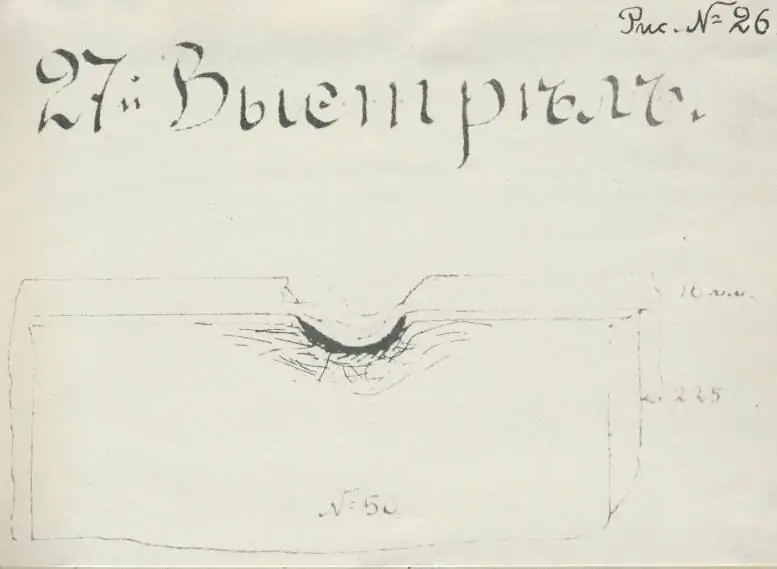
Teljesen tisztázatlan, hogy mi történhetett itt. Elsősorban azért, mert nem világos, hogy pontosan hol találta el a héj. Először is, az "él" maga is kiterjeszthető fogalom, mivel többek között arra is használható, hogy "valaminek a szélét" jelölje. Vagyis még az sem világos, hogy a lövedék középvonala a páncéllemez függőleges vagy vízszintes felületét érte -e.
Kiváló minőségű biztosíték jelenlétében azonban ezen lehetőségek bármelyikétől sokkal nagyobb kár várható. Ha a lövedék a páncél függőleges síkjába ütközött, akkor annak teljes mélységében össze kellett omlania, nem pedig 75 mm -rel. Ha az ütés a vízszintes részre esett, akkor miért rögzítik a jelentésben az akadály találkozási szögét 65 ° körül? A lövedék nem esett az égből a 225 mm-es födém vízszintes felületére, a függőleges felülethez képest 65 ° -os szögben lőtt, ami azt jelenti, hogy 25 ° -nak kellett volna lennie a vízszinteshez képest. Ebben az esetben visszapattanásra számíthat. Vagy (lövedék szétrobbanása esetén) a 225 mm -es páncéllemez felső élével szomszédos vízszintes 37,5 mm -es páncél fedélzet sérülése. De ebből semmi sem történt.
Véleményem szerint a hiba egy meghibásodott lövedék volt, amely ütközéskor összeomlott, ezért a robbanás nem teljes erővel sikerült. Vagy talán egy hibás biztosíték, amely felrobbantotta a "nagy robbanásveszélyes" pillanatot, amikor a lövedék hozzáért a páncélhoz. Az is lehetséges, hogy a lövedék nem hibás, hanem összeomlott, mert a páncéllemez két felülete által alkotott szög egyfajta „hasító” szerepet játszott. Formálisan a lövedék nem hatolt át a 225 mm -es lemezeken. De a találat következményeinek rendkívüli szokatlansága kapcsán véleményem szerint az okot nem a páncéllemez ultramagas tulajdonságaiban kell keresni.
Következésképpen a "kizárt 4. számú edény" 225 mm-es páncéllemezeinek ágyúzásának eredményei nem erősítik meg vagy cáfolják korábbi következtetésünket.
A hazai lövedékek és páncélzatok azonban más mérföldkőnek számító tesztekre is sor kerültek 1920 -ban. Itt teljesen más volt a cél. A kísérleti rekeszt a cár-atya uralkodása alatt építették, hogy meghatározzák az optimális védelmi rendszert a jövőbeli orosz rettegések számára. De 1917 -ben valami baj történt az oroszországi önkényuralommal. A dreadnoughtek építésére irányuló projektek pedig a kivetítés kategóriájába kerültek. Ennek ellenére a vizsgálatokat elvégezték, beleértve - 305 mm -es 470, 9 kg -os kagylók felhasználásával. Az eredmények nagyon érdekesek. De erről a következő cikkben beszélünk.
De amit külön szeretnék megjegyezni, az egy kirívó furcsaság jelenléte a tesztekben. A tény az, hogy szándékosan túlbecsülték a tüzérségi tűz távolságát.
Így például a 225 mm-es páncélzatú lövéseknél, páncéltörő héjakkal, azt jelzik, hogy a lövedék paramétereinek megfelelő távolság 65 kábel. De ez nem igaz - 557 m / s sebességgel, a normálistól 25 ° -os eltéréssel, egy 305 mm -es lövedéknek körülbelül 8% -kal vastagabb páncélzatot kellett áthatolnia, mint 65 kábellel történő tüzeléskor, ahol a lövedék sebessége 486,4 m lenne, és az eltérés a normálistól - 10, 91 °.
Természetesen banális hibára lehet gyanakodni a cikk szerzőjének, vagyis nekem. De akkor hogyan kell megérteni a lövöldözőtorony tüzelését - itt a dokumentumokban a lövedék sebessége ugyanazt jelzi, mint 557 m / s eltérés a normálistól - csak 10 °, de a távolság azonosnak tekinthető, azaz 65 kábel ! Más szóval kiderül, hogy a "megfelelő távolságot" egyáltalán megadták a beesési szög figyelembevétele nélkül, csak a lövedék sebességét tekintve?
Ez a verzió azonban könnyen ellenőrizhető. Számításaim szerint 60 lövedék lövedéksebessége 502,8 m / s, 80 kábel esetén 444 m / s. Ugyanakkor a 305 mm / 52 löveg távolsági lövöldözésére vonatkozó adatokat L. G. Goncsarov ("A haditengerészeti taktika folyamata. Tüzérség és páncél", 35. o.), Ezekre a távolságokra 1671 és 1481 láb / s, azaz a metrikus rendszerbe lefordítva - 509 és 451 m / s.
Így feltételezhetjük, hogy számológépem továbbra is lefelé mutat egy bizonyos hibát, amely 6-7 m / s. De nyilvánvaló, hogy az 557 m / s 65 kábel és a 457 m / s 83 kábel esetében itt szóba sem jöhet.
És még egy tény, ami elgondolkodtat. Mint látható, összesen 7 db 305 mm-es páncéltörő lövedéket lőttek ki 225-250 mm-es páncélzatra. Ugyanakkor a tüzelési feltételek olyanok voltak, hogy a meghatározott páncélzatnak jelentős különbséggel kellett áttörnie. Ennek ellenére a valódi lövöldözési körülmények között, még hatótávolságon belül is, csak hét esetben ötször hatolt át a páncél. És csak 4 kagyló haladt belül.






